tezomeya ブログ

本当に無駄なお話 ~『インターステラー』を観ての科学考証的壱考察
※おことわり※
何人かの方にご指摘いただいた通り、本テキストの科学考証は間違っております。
本来ならばカー解を使用しなければいけない所、シュバルツシルト解で計算しております。しかもその計算も間違えている可能性もございます。
素人の勇み足で申し訳ありません。
その点を御含み頂き、もしよろしければご覧ください。
2019年正月 管理人 青木正明
ずっと気になってた映画、『インターステラー』をやっと観た。
一昨年からずっと気になっていながら忙しくて映画館に足を運べず、その後もdvd借りたりする機会がなくてやっと今日の昼に視聴した。比較的長い映画なので、時間が取れる日を探して、だ。
感想としては、まぁ、面白かった。
ただ、正直言って結構残念だった。
この映画をことのほか楽しみにしていたのは、前評判として科学的背景がとてもしっかりしていて、特に相対性理論を駆使した話というふれこみだったからだ。クリストファーノーラン監督の映画が特段好きという訳ではないが(メメントは結構好きだった)、最近珍しいハードコア系SF映画ということで、例えばグレッグ・イーガン(オーストラリアの超ハードコアSF作家)バリのゴリゴリのSFネタを期待していたのだが、そうではなかった。
確かに、“特異点”とか“事象の地平面”とか、相対性理論で使用される用語が正しく(って素人の当方レベルの判断だが)使用されていたし、映像もなんかそれっぽかった(大質量ブラックホールのエルゴ球の表現とか)。
だけど、愛の力は時空を超えるとかの話がメインテーマになってしまったりとか、重力にかかわる方程式が解けてないのに解けてるふりを40年もしてたりとか、さらに事象の地平面での量子データが得られて(それもモールスで!)すぐに新たな重力方程式ができて重いもん飛ばせるようになるとか、説明なく短絡的過ぎてわけがわからない。
ハリウッド映画特有の「こまけぇところはいいんだよっ!」的なところがやっぱりこの映画にもあって、とても残念だった。
いや決してヒューマンドラマが嫌いなわけでもなんでもない。そもそも、SFってのは、作者が自由に世界観を作りたいがための空想世界なわけで、そこに完全なる整合性がないといけないわけでないということは当方も理解しているつもりだ。
ただ、この映画の前評判が、「科学的背景がとてもしっかりしている」「著名な理論物理学者が科学側面のコンサルタントを全面的に請け負った!」なんていうもんだったからそのあたりものすごい期待してたんだけど、そこにとてもがっかりしただけだ。
ごはんで例えるなら、すごい本格的なインド宮廷料理屋さんって触れ込み聞いて行ってみたら、スパイスたくさん使ってるらしいけど全然それがわからないフツーに美味しいココ壱カレーみたいのが出されていやそれも嫌いじゃないけどなんだかなぁ、、みたいな。
そんな、有名な科学者がバックについた映像なんていわれたら、僕らの世代はもう「COSMOS」とかを連想しちゃうじゃないですか。期待しちゃいますよねぇ。
さっきも挙げた通りいくつか気になる点はあったのだが、特にあれ?って思ったところは、最初に着陸する惑星の話。
大質量ブラックホールを太陽とする惑星で、ブラックホールのあまりの重力のために時間の進み方が遅すぎる、というところ。
水に満たされた、地球とほぼ同じ大きさ(この惑星の重力が地球の1.3倍っていうセリフがあったので)の惑星の1時間が、地球のなんと7年になるというのだ。 ほんとにそんなことがありうるのか。観てて直感的におかしいだろと思ったんだけど、それをこれから検証しようかな、と。
・・・というわけで、さぁこれからただの暇つぶしのはじまりはじまり。ものっすごいお暇な方、もしよろしければどうぞお付き合いください。
※ご注意※
このあたりから間違った解釈をしております。
ワームホールを経由して地球外惑星を探しに行った宇宙探検飛行士たちはまずこの、海に満たされた地球よりほんの少しだけ大きい惑星にたどり着く。

この惑星の時間の進み方は極めて遅い。さっきも言ったとおり太陽であるブラックホールがあまりに重くあまりに近いところを回っているため、その強力な重力のせいで、この星の1時間が地球の7年に匹敵すると映画の中で科学者の飛行士が説明し、惑星に向かう前に皆は無駄な時間をすごしてはいけないと気を引き締めるのだ。
アインシュタインが1915年に発表した一般相対性理論によると、重力の強いところでは重力の弱いところに比べて時間が遅く進む。これは本当で実生活にも応用されています。例えば、地表にいる私たちとはるか上空を飛んでいる人工衛星では時間の進み方が違う。地球からの重力が地表の私たちより弱い人工衛星のほうが少しだけ早く時間が進むために、人工衛星に乗せている時計はわざと少しだけ遅く進む設定をしている。
そして、時間がどの程度遅くなるかという計算は、アインシュタインがだしたアインシュタインの重力方程式というもので計算できる。
こんな式です。
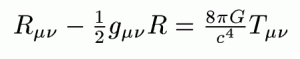
当方はこの式の意味がさっぱりわかりません。
でも、これをもっとわかりやすい形にしてくれたシュヴァルツシルトさんっていうドイツ人がいらっしゃいまして、この人の式だとちょっとわかりやすくなる。いわゆるシュヴァルツシルト解っていうんだけど、こんなの。

これを使って、はたしてそんな太陽系が存在するのか計算してみた。
・・・・・ややこしい途中の式は省きます。こんな感じ。酒とチョコにお手伝いしてもらってちまちま計算しました。

で、出たのが、こんなに進む時間が遅くなるためには、この惑星はブラックホールの半径の本当にすれっすれを回っていないといけなくて、それは、ブラックホールの半径の1.00000000029倍が公転半径になる、ってことになりました。
これ、もしブラックホールが私たちの太陽と同じ半径だったとしたら、太陽の表面から20cmのところを回ってる星ってことになります。ありえないね。もう。でも宇宙では何が起こるかわからんのでまだまだ計算します。
このブラックホールの半径の0.00000000029倍が、惑星の半径より大きかったらありえるよね。
ここで念のために補足します。物理で言うところの物体同士の距離というのはお互いの重心からの距離です。なので、2つの物体の距離が2つの物体の大きさよりも小さいというのは、どちらかにめりこんでるということ。だから、物体がふたつとも球であれば、それぞれの半径の足し算以上の距離がないとだめということです。
今から計算しようとするのは、惑星の地表とブラックホールの表面(これが事象の地表面ってやつですが)が本当にすれっすれで回る状況を想定しているわけです。
で、映画の中でこの惑星は重力が1.3倍っていってたので、この惑星が地球と同じように地殻型惑星として(すなわち密度が地球と同じと考えて)ニュートンの方程式から計算するとこの惑星の半径は約7100km。
ということは、さっきの数で割ると、このブラックホールの半径はなんと24兆km。これは約2.5光年です。もちろん私たちの太陽系の半径なんて優に超えてます。そしてこのブラックホールの質量もさっきのシュヴァルツシルト解から計算すると約1.7×10の43乗kg。これはざっくり太陽の10兆倍の重さで、私たちが住む銀河系の全質量より重いです。
私たちの銀河系のようにちゃんとした銀河や星雲の中心には、とてつもなく大きいブラックホールがどうもあるらしいので、とんでもないブラックホールがあってもおかしくないかもだけど、今知られてる限りで一番大きい超大質量ブラックホールが太陽の約180億倍。映画のブラックホールはこれのさらに500倍以上です。
うーん、もうしわけないけど、やっぱり直感あたってたっぽい。ありえないかなぁ。
しかもしかも、この星に降り立った飛行士たちはなんだかんだ惑星でひと悶着あって4時間ほど過ごしてしまう。で、命からがら惑星を脱出した後は、外で待っていた母船にさっくりと戻る。戻ってみると、そこで待ってたクルーが「もう、まちわびたよ・・」なんて二十数年待って白髪混じりの頭になってた。すなわち、この母船はブラックホールからはるか離れた重力の弱いところで待ってたことになってて、その距離を計算してみると、少なくともこの惑星からさらに何十光年も離れてないといけないんだわ(ざっくりなのは、母船のクルーが待ってた年数がざっくりなので)。
すくなくとも彼らの宇宙船は光速の何パーセントとかでは飛べない(地球から土星に行くまで2年かかってる)ので、何十光年なんていう距離を“さっくり”戻ることは不可能。ここもおかしい。
うーん、やっぱり、ありえないなぁ。
グレッグイーガンや昔のアーサーCクラークさんの話だったらこの当たりもう少しちゃんとしてると思うんだけどなぁ。。
残念だなぁ・・・・。
・・・と、ただの重箱の隅突っつきネタでした。
でも、よく考えてみたら、こんな長ったらしいブログを書く動機を与えてくれたのはこの映画なわけで、そういう意味では、なかなか素晴らしい刺激だったのでしょう。これだけでも観た価値があったのかも。
お付き合いくださりありがとうございました(って付き合ってくれた人いたんだろうか・・・)



最近テレビで見て、おもしろかったけど違和感があったので捜していたらここにたどり着きました。
難しい計算はわからないけれど、水の惑星に最初に行った人は数時間か数日の滞在だったということで、発信された電波も数日分だけのはず。でも受信側では何年分も受信していたような描写だったかなと。そこからはその世界の理論ではそれが正しい(トップをねらえ的な)として楽しんだのでした。投稿主様がここを維持していて下さったおかげで、他の方の感想も見られてよかったです。
コメントありがとうございます。
最近テレビでやっていたのですね。
このブログが何かのお役に立てたのならとてもうれしいです。
自分も、このブログにコメントいただくたびのハラハラ感を楽しめるようになってきております。
本業とは全く関係ありませんがおそらく死ぬまで閉じないと思います。
エゴやプライドが滲み出てて読んでて苦痛だった
ちまちま保険かけずに堂々と書けいい!
インターステラーはとても良い映画でした
お気を悪くさせてしまったご様子、大変申し訳ありませんでした。
深くお詫び申し上げます。
科学にフワッとした知識しか無い自分でも、本文やコメントのやり取りは大変刺激的でした。ここなら他では伺えないこともご教示いただけるのではと思い書かせていただきます。ガルガンチュアのスイングバイの段階でさえ数十年のタイムラグが表現されており、その後母船から離脱したクーパーは事象の地平面に落ち込んで行く訳ですが、中心部の未来人の次元に辿り着く前に、地平面を越えている表現が見られることから、クーパーは巨大な重力の影響で無限に等しい時間、地平面に囚われてしまったのではと思うのですが、その点についてはこの映画はどう解決しているのでしょうか?例えば無限に等しい時間、地平面に囚われた後、未来人の次元から解放される際に時空を超えて、過去の木星近辺まで転送されたと捉えれば良いでしょうか。前提にも誤った認識があるかもしれませんが、何卒ご教示いただければありがたいです。
本業がバタバタでお返事遅くなってしまいすみません。
前提として、このあたりの理論物理学に関しては私も全くの素人ですので、ちゃんとしたお答えなど当然できないのですが、
お話を伺っての私の勝手な推測としては、なにぶん事象の地表面では私たち人間の官能的反応としてどのようにとらえられるのかは全く不明のことばかりでしょうし(そもそも生命維持できない可能性高いですし)、その向こう(すなわちおっしゃっておられる中心部?)といった三次元的なものの捉え方も正確かどうかもわかりませんし、言ってみれば「なんでもあり」なのだろう、と思いました。
なので、なんでもアリなのでしょうけど、この映画のストーリーとしてそこに家族愛が重要な要素として関わってきて、で、いろいろあってクーパーが私たちの現実世界に戻ってこれた、というのがちょっとかゆいな、と思った次第です。
すみません、全然答えになっていないと思います。
どなたか、正確な知見をお持ちの方でお答えいただけるようでしたらぜひお願いいたしますm(__)m
主様と似たような違和感を覚えて辿り着きました。
結局のところこの映画は、事象ごとに切り分けたときの数字上の正しさは担保されていても、全体として納得させるだけの表現はできていなかったように感じました。
前者は視聴者を驚かせるSFギミックとして役立ちますが、後者が基盤にあってこそではないかと。後者にケチがつけば自然と前者にも疑義の手が伸びるわけです。ピーキー理論前提のSFならますますそうなる。
エルゴ球や津波の描写には楽しませてもらいましたが、そもそもあの星に降り立ってしまう時点で違和感に飲み込まれてしまいました。
とはいえエンタメとしては楽しませてもらいました。
失礼します。
コメントありがとうございます!
おっしゃる通り、あの星に降り立った(普通に水が液体として存在する環境温度であるとか、津波は起こるけど地面からは引っぺがされるほどではないとか・・)時点で、違和感ありますよね。
そして、最後の「エンタメとしては楽しませてもらいました」にも激しく同意です【^^】
結局、私はこの映画7回くらい見ておりますのでwww
つい先日youtubeで中学数学からはじめる相対性理論という動画をみて、そういえば相対性理論を扱った映画をみたことあったなと久しぶりにインターステラーを見たものです。
当時はわりと適当に流し見みしていてあまり深くみていなかったのですが、少し前提知識を入れて見るこの映画は大変楽しめました。ただ、1時間が7年?しかも重力は1.3倍?どういうことなんだろうと検索してこちらにたどり着きました。
私の理解力ではこちらを読んでもふんわりそいうこともあるのかな程度でしたが、大変ありがたい記事です。コメントも一部心無い方もおられますが概ね理知的な方でコメント読むのも楽しめました。
私個人の考えとしてはこういう検証や疑問を考えることは非常に楽しいことで、映画が終わったあと調べたりすることが多いです。ただ、ブログ主さんのようにそこまでガッツリやることはないですがw
見た映画を100褒める見方もあるとは思いますが、こういった思考遊びみたいなのも楽しいものですよね。
コメントありがとうございます!
思考遊び(というほど正確な計算ができているわけではないですが)にお付き合いいただき嬉しいです。
私としても、このブログは本業とは全く違うジャンルにおける一杯の三ツ矢サイダーみたいなもんでして、うれしいコメントもそうでないコメントも含めてとても楽しませていただいております。
ちなみにですが、私も全然物理は素人でして、おそらく匿名様と同じく中学数学の三平方の定理による特殊相対性理論程度しか理解できていませんですハイ^_^;
じゃあお前がもっと面白い映画作れよ
そんな大それたことはもちろんできませんです。
力ないものが偉そうにのたまってしまい申し訳ありませんですm(__)m
科学的知見を全く持ち合わせない私でしたが、この映画はとても面白い映画でした。
この記事のシュバルツ解?なるものでお確かめになった科学的なプロセスも楽しめました。
これもSF映画の楽しみ方の一つですね。羨ましいです。コメントでの指摘を踏まえ、誤りを明示しつつこの記事を残された主様の姿勢もまた科学的ですね。
大それた映画を作るのは無理だとしても、とても面白いブログ記事を書いてくださいました。感謝てす!!
こんにちは。書き込みありがとうございます。
お返事が遅くなってしまい申し訳ありませんでしたm(__)m
過分なるお言葉恐縮です。
調子に乗らないよう気を引き締めて余生を送っていきたいと思いますm(__)m
ノーラン監督作品は論理的で複雑なシナリオで作られることが多いですが、現実性という意味ではかなりぶっ飛んでいるものが多いですね。
なまじ絵や音が真面目なのでリアルな映画と思いがちですが、自分は基本的にはファンタジーだと思っています。
作っている側もある程度の嘘は承知で「この世界ではこう」というような、かなりゲーム的な解釈で世界観を設定していると思われるので、観る方もああそうなんだなとざっくり構えたほうが観やすいのも確かでしょう。
もちろん、インターステラーは宇宙や相対性理論というような題材を扱っているので、科学的なツッコミはもっともですし、面白いのでどんどんやってほしいです。
記事を読んでいて、昔好きだった空想科学読本という本を思い出しました。
こんにちは。書き込みありがとうございます!
お返事が遅くなり申し訳ありません。
おっしゃる通り、広いココロで見ることが大切ですよね。
このブログは了見の狭い自分に対しての良き指導の場となっております。
本当にいろいろ皆さんご意見ありがとうございますです。
空想科学読本、私は知らなかったのですが、90年代のものだったのですね。私が若いころは学研の科学でしたwww
最近、テネットを観て、そこからインセプション、インターステラーを観た者です。
思ったのは、監督、物理学好きなんだろうなあ!!っていうフワフワした感想でした(笑)
私も好きです。しかし理解力はないので、感じるだけです。特に津波とブラックホールの環?のシーンが好きですね〜。ワクワクします。
違和感も感じますが、そこは考察サイトを見て楽しんでます。ありがとうございました!
あ、あと難しい物理学とエンタメを融合させた監督にもありがとうを言いたい(笑)
もっと物理学とかに興味を持つ人が増えて、戦争なんかより宇宙に行ってほしいなあー!死ぬときにブラックホール葬も楽しそうです。痛いのは嫌だけど。
書き込みありがとうございます!
あ、いえ、私も全くの素人でして、単に物理や化学ネタが入った話が好きなだけです、ハイ【^^】
テネット、まだ見ていないのです。見ますね!